1.3 Let us start with something familiar, the Sun-Earth system

Fill out the following (feel free to Google):

Radius of Sun (\(R\))	\(6.96\times10^{8}\) m
Average distance from Sun to Earth (\(R_{e}\))	\(1.50\times10^{11}\) m
Mass of Sun (\(M_{s}\))	\(1.99\times10^{30}\) kg
Mass of Earth (\(M_{e}\))	\(5.97\times10^{24}\) kg
Gravitational constant (\(G\))	\(6.67\times10^{-11}\) m3kg-1s-2
Linear momentum of Earth (\(p_{e}\))	\(3\times10^{4}\) kg ms-1

(We can get \(p_{e}\) by knowing that the Earth circles around the Sun in about 365 days. How?)

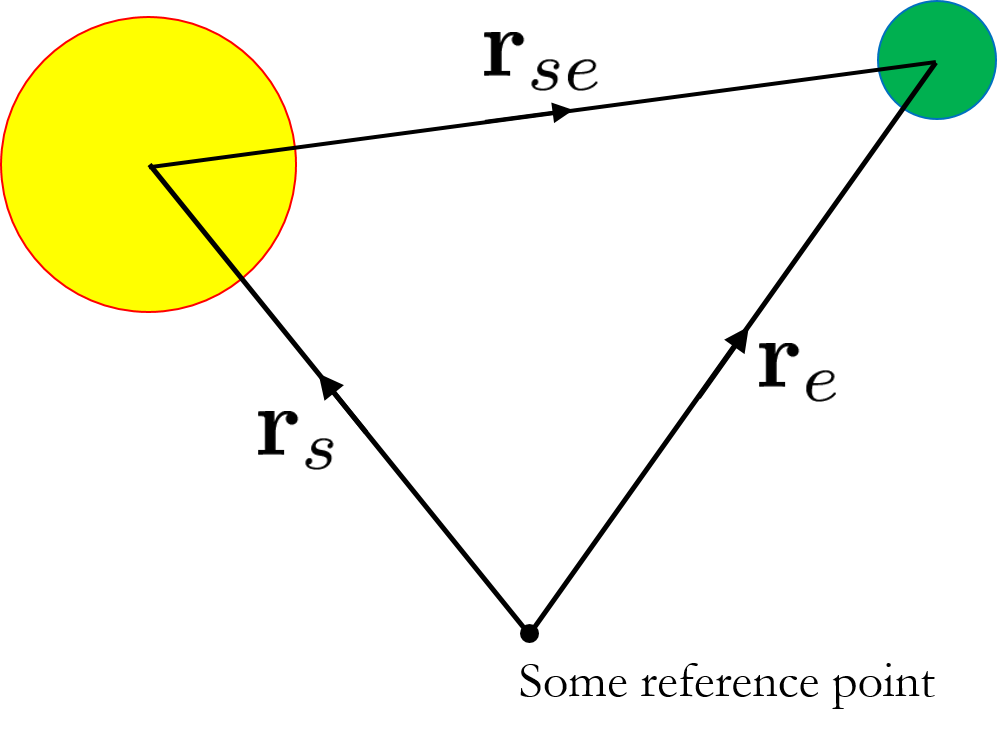
Let \({\bf r}_{s}\) and \({\bf r}_{e}\) be the position vectors of the Sun and Earth respectively. Express \({\bf r}_{se}\) in terms of the two postition vectors. \[ {\bf r}_{se}={\bf r}_{e} - {\bf r}_{s} \]

Newton’s Law of Gravitation:	\(\displaystyle {\bf F}=-\frac{GMm}{r^{2}}\hat{{\bf r}}\)
Force that the Sun exerts on the Earth:	\(\displaystyle {\bf F}_{se}=-\frac{GM_{s}M_{e}}{r^{2}_{se}}\hat{{\bf r}}_{se}\)
Force that the Earth exerts on the Sun:	\(\displaystyle {\bf F}_{es}=\frac{GM_{s}M_{e}}{r^{2}_{se}}\hat{{\bf r}}_{se}\)
Newton’s second law (express in terms of rate of change of momentum)	\(\displaystyle {\bf F}=\frac{d{\bf p}}{dt}\)

Applying Euler’s scheme for solving differential equation numerically

\[ \begin{align*} d\textbf{p} &= \textbf{F}dt \\ \textbf{p}_{i + 1} &= \textbf{p}_{i} + d\textbf{p} \\ &= \textbf{p}_{i} + \textbf{F}_{i}dt \end{align*} \]

Relationship between momentum and position vector is given by:

\[{\bf p}=m{\displaystyle \frac{d{\bf r}}{dt}}\]

Applying Euler’s scheme for solving differential equation numerically.

\[ \begin{align*} d\textbf{r} &= \frac{\textbf{p}}{m} dt \\ \textbf{r}_{i + 1} &= \textbf{r}_{i} + d\textbf{r} \\ &= \textbf{r}_{i} + \frac{\textbf{p}}{m}dt \end{align*} \]

We will discuss the above briefly in class and do part 3 together as a group.

To be continued…