classical mechanics continue to baffle scientists – a simple chain problem?
Fields covered: Statistics, Probability, Physics
Related Articles:
§ ![]() Understanding the chain fountain
Understanding the chain fountain
After more than 300 years after the Newton’s laws of motion were published, modern scientists should know everything there is to be known about classical mechanics by now, don’t you think? Well, in February 2021, popular science YouTuber Steve Mould published a viral video of a chain rising out of a beaker as it is falling out of it. He dubbed this novel phenomenon the Mould effect[1].
Scientists quickly got to work, with a paper being published in 2014 by Cambridge University explaining what they think is going on behind the ‘chain fountain’[2]. Here’s a rough explanation.
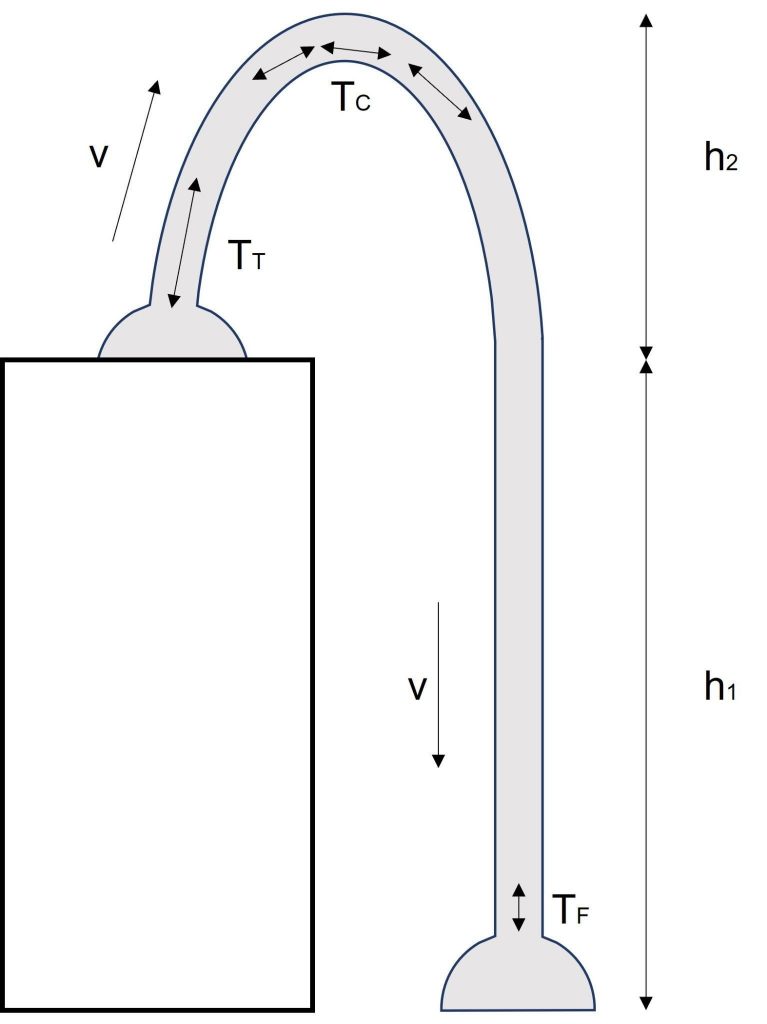
In their model (Figure 1), a chain of mass per unit length λ, is resting on a flat table a distance, h1, above the floor. Assuming the chain to be in a steady state, it “flows” to the floor with speed, v. The tensions in different sections of the chain are denoted by TC, TT and TF. Since the chain fountain rises even before contact with the ground, TF is clearly zero.
Here comes one surprising fact. The centripetal acceleration provided by TC is usually much larger than the force due to gravity. This causes the TC to be roughly equal to the centripetal force and hence independent of the chain’s curvature! Good news though, this part is already well studied and has been known since the mid-1800s[3]. We can easily show that TC=λv2.
Here comes the important part. We consider how the force is balanced out at the chain just above the table and at the curve during the steady state. For a small change in time Δt, the mass picked up by the chain will be λvΔt. Since momentum is mass times velocity, this makes the gain in momentum equal to λv2Δt. This change in momentum was concluded to be due to TT, the tension right above the surface and TT= λv2.
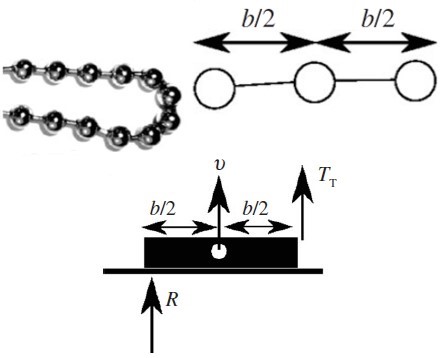
If you’re observant, you might have realised something very wrong at this point. If TCC=λv2 and TTC=λv2 as well, then the forces are already balanced. The chain shouldn’t rise at all! But we clearly saw the chain rise, so what’s going on here? The trick is that as the chain rises, the chain that gets picked up form a lever when the beads compress together (Figure 2).
This causes an anomalous upwards force R to be exerted, offsetting TT. Since TC now exceeds TT, the chain will rise as it is pulled upwards by TC. Thus, the mystery of Mould effect has been solved. Or has it?
The beauty of science is that anyone with enough knowledge on the basics can try to figure out what’s going on for themselves. Recently in July 2021, another popular science YouTuber disputed this claim, arguing that there is no need for an extra force R and that the existing momentum of the chain is already enough to cause the Mould effect[4]. It remains to be seen whether there was a wrong assumption in the Cambridge scientists’ model.
Physics in our daily life is quite amazing, a seemingly simple classical mechanics phenomenon such as the Mould effect behaves in such an unexpected way. I encourage you, the reader, to think of a possible explanation and try to conduct experiments to understand what’s going on for yourselves. Who knows? Maybe you will accidentally discover a new phenomenon and name it after yourself!